main-written1

Written assignment 1, due Wednesday, September 22nd.

The goal of this is to give you some practice working with linear transformations.

Note: if you want to turn this on “typed” (via email), you do not need to include the sketches for question 2 (all other answers are just text).

To turn things in by email, send it to the TA (sghosh@cs), be sure to make the subject line be your cs id and “Written 1” (so for me, it would be “gleicher Written 1”)

Otherwise, you can give it Subhadip on paper, or put it in his mailbox on the 5th floor of CS. Note: you might not be able to get to his mailbox after 5pm unless you have a building access key.

We actually prefer email submissions.

Question 1

The standard OpenGL coordinate system (called “Normalized Device Coordinates”) put 0,0 at the center of the screen. Has X going to the right, Y going up, and Z coming out of the screen (its right-handed). The range along each axis is from -1 to 1 (so -1,-1,0 is the lower left corner of the screen). You get this coordinate system when you have the identity matrix atop the matrix stack (using glLoadIdentity).

Suppose we want a transformation that makes the lower left corner of the screen (0,0,0) and the upper right corner of the screen (640,480,0). (the Z values should not be changed). There is an OpenGL function called glOrtho for doing this, but we won’t use it in the this question.

Part A Provide a sequence of openGL commands that set up this coordinate system (it should be a sequence of translations, rotations, and scales).

Part B Reverse the order of the transformations in your answer to 1A. This program would give a different result. Change the parameters to the functions so that it gives the same transformation as in 1A. (note: there were typos in a previous version)

Question 2

Here’s a little open GL function that draws a “house shaped” object that is articulated:

    void glHouseArm(float angle1, float angle2) {
        glPushMatrix();
        glRectf(0,0,1,1);
        glTranslatef(0,1,0);
        glRotatef(angle1,0,0,1);
        glRectf(0,0,1,1);
        glTranslatef(0,1,0);
        glRotatef(angle2,0,0,1);
        glBegin(GL_TRIANGLES);
        glVertex2f(0,0);
        glVertex2f(1,0);
        glVertex2f(.5,.5);
        glEnd();
        glPopMatrix();
    }

Part A: Sketch what this would look like if angle1 = angle2 = 0. What would the position of the tip of the triangle be?

Part B: Sketch what this would look like if angle1 = 90, and angle2 = 45. What would the position of the tip of the triangle be?

Part C: Write an equation that computes the position of the tip of the triangle given the two angles.

Question 3

For the following questions, consider a simple graphics toolkit that works like OpenGL (that is, it has a matrix stack, and the transformation commands post-multiply themselves onto it):

• Translate(x,y) @ post-multiplies a translation matrix onto the top of the matrix stack
• Rotate(a) @ rotates (counter clockwise around the origin) by a degrees
• Scale(x,y) @ scales by x and y.
• ReflectY() @ reflects around the Y axis (note: this changes the X positions)
• Push() @ pushes a copy of the top element on the matrix stack
• Pop() @ removes the top element from the matrix stack
• Block(letter) @ draws an @alphabet block@ with the letter inside. The block is a unit square, with its lower left corner at (0,0) and its upper right corner at (1,1). You can assume that the letter A is symmetric about its vertical center, and the letters B, C, D and E are symmetric about their horizontal centers.

For example, this program:

    Push
    Translate(2,2)
    Block(@A@)
    Pop
    Rotate(90)
    Block(@B@)

Produces this picture:

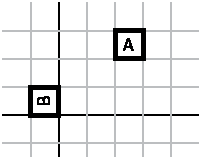
Question 3A: Write a program that produces that picture without using any push/pop commands.

Question 3B: Write a program that produces the picture here without using the push/pop commands:

Question 3C: Write a program that produces the same picture with push and pop commands. Write your program in a way that if you needed to change it to reposition one of the squares (without effecting the other two, or the sizes of any of them), you would only need to change one line of the program.

Question 4

For each of these two cases, you need to give a 3x3 homogeneous transformation matrix that maps the triangle given to the triangle (1,1) (2,1) (1,2). Note that each of the following is something you’re transforming from.

Question 4A: (0,0), (1,0), (0,1)

Question 4B: (1,0), (2,0), (1,1)

Question 4C: (0,0), (4,0), (0,3)

Question 4D: (1,1), (2,1), (2,2)